橙的核电站

我的铍振荡器去哪了

0%

图像抖动及其应用

发表于 分类于

title

这是CNPP的《数字图像分析》课程大作业的文稿。

1.抖动简介

在计算机以及数字信号处理技术发展，有限的数据位宽带来了量化误差，在相当一段时间内制约着数字系统的精度以及效果。而抖动（Dither）则是一种对信号人为加入噪声，以使量化误差随机化的手段，以避免大片不自然的信号出现。

最早对抖动的应用可追溯至第二次世界大战。当时，轰炸机使用装有成百上千齿轮的机械计算机进行导航和弹道计算。事实证明这些仪器在空中比在地面上表现得更为准确。工程师意识到这是因为飞机的振动使得哪些传动部件由短促的抽动变为了更加连续的运动，从而减小了行程的误差。于是他们特地在计算机中安装了振动电机以提高精度，同时，这种振动手段也被称为“dither”——源于中世纪英语动词“didderen”。如今，当你敲动机械仪表想让它指示得更准确时，其实就是在利用抖动。在现代的词典中，“dither”被定义为紧张、混乱或激动的状态，不过在此处，它是件使数字系统更接近模拟现实的好事。

— Ken Pohlmann, Principles of Digital Audio [1]

下图：诺顿光学轰炸瞄准具，以及其装备于投掷“小男孩”原子弹的伊诺拉·盖伊号B-29轰炸机。
1-1
1-2

此后，抖动技术应用于了数字音视频、地震信号处理、天气预报等诸多领域。

抖动技术的理论依据在于，量化过程产生的误差大多相关于原信号，这就会使得误差具有周期性或可预测性。在很多领域，周期性噪声会带来明显的不良影响。例如，人耳具有类似傅里叶变换的分辨能力，当音频中存在周期性误差时，就相当于额外增加了一个频率的声音，倍明显感觉。若使用抖动将这一误差随机化，其就难以倍人耳分辨[2] [3] [4]。

2.图像抖动的发展

人类对美的追求一向挑剔，对图像显示技术的诉求亦孜孜不倦。然而，存储一幅绚丽的图像的代价是难以想象的。以常见的1024*768分辨率大小的屏幕为例，显示RGB565格式的彩色信号，则一帧所占用的存储空间计算如下：

1024×768×16bit8=1,572,864Byte\frac{1024\times768\times16bit}{8}=1,572,864Byte

而对于早期的家用计算机，内存资源十分紧张（几十kByte左右），同时，当时的视频芯片通常没有独立的显存，需要与系统内存共用，这就决定了当时的计算机无法使用非常丰富的色彩。在那时，诞生出了颜色单元法（Color Cells）、NTSC伪色法（NTSC Artifact Coloring）、CPU驱动图形法（CPU Driven Graphics）等在较弱硬件机能下显示尽可能多色彩的方法。

GBA掌机的屏幕可以显示15bit色彩（32768色），但限于存储空间，在每一块特定大小的区域中不会有太多颜色出现。

2-1

在这样的条件下，抖动技术被广泛使用，来在各阶色彩间产生平滑过渡，或是当作灰度来使用。

PC98，《玛丽亚的民谣》，使用规则抖动（Ordered dithering）实现天空的灰度渐变

2-2

2-3

PC98，《大航海时代2》，使用规则抖动在色彩间平滑过渡

2-4

2-5

使用了相同的色彩，效果却截然不同，左侧：直接量化；右侧：Floyd–Steinberg抖动

2-6

PS1，《寂静岭》，使用了硬件进行规则抖动

2-7

随着硬件性能的逐渐提升，显示器可以显示更多的色彩，电脑存储器也拥有了更大的空间，抖动技术便已不再必要。不过，在现在的许多便携设备上，显示器件、容量与功耗依然是分寸必争，图像抖动依然有广泛的用武之处。

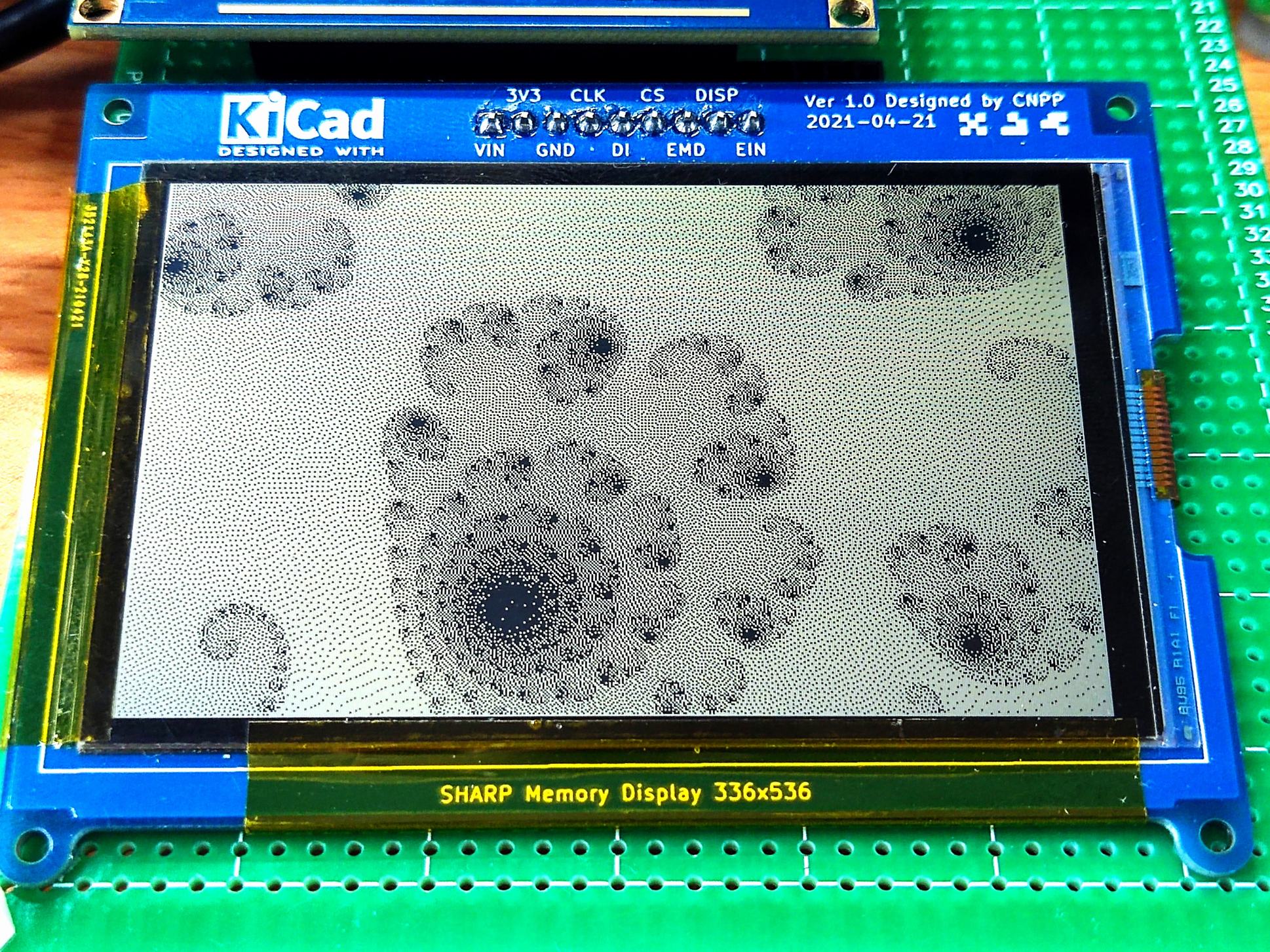
例如下图所示的夏普LS032型MemoryLCD屏幕，是目前较为先进的一种低功耗LCD显示器件。其拥有分辨率高，像素密度高，刷新速度块，静态功耗极低，对比度强等特点。

2-8

美中不足的是，它只能显示黑白二值的像素，不具备灰度功能，但若能合理运用图像抖动，便也能取得不错的显示效果。这也是接下来抖动算法实践的实用目标。

2-9

3.图像抖动算法

根据维基百科的介绍，图像抖动主要有阈值抖动、随机抖动、规则抖动、Floyd–Steinberg抖动等[5]：

3-1

其中，阈值抖动是最简单的抖动算法，它是将每一个像素的灰度与一个固定的值比较得来的，与图像二值化相似，同时，也丢失了大量的细节；随机抖动则是与一个随机的阈值进行比较，这也是最初“抖动”的思路。图中的半调抖动与Bayer抖动同属于规则抖动，其使用以某种规则变化的二值矩阵代替原图中的灰度像素，前者依然应用于印刷业，后者则常见于古董计算机及老游戏。Floyd–Steinberg抖动是一种基于误差扩散思想的算法，有着很好的效果，并衍生出了数种从速度或锐度角度优化的算法。此次主要探究的是Bayer抖动算法和Floyd–Steinberg抖动算法。

3.1.Bayer抖动

Bayer抖动需要先从狭义的规则抖动说起，它的原理十分简单：假若只有黑白两种颜色可供使用，那要是想得到灰度效果，就用一个N×NN{\times}N的二值矩阵来替代原来的灰度像素，根据原灰度数据调整矩阵中“0”、“1”的数量占比，这样组合之后，从宏观上观察便能体现出模拟灰度的效果。

3-2

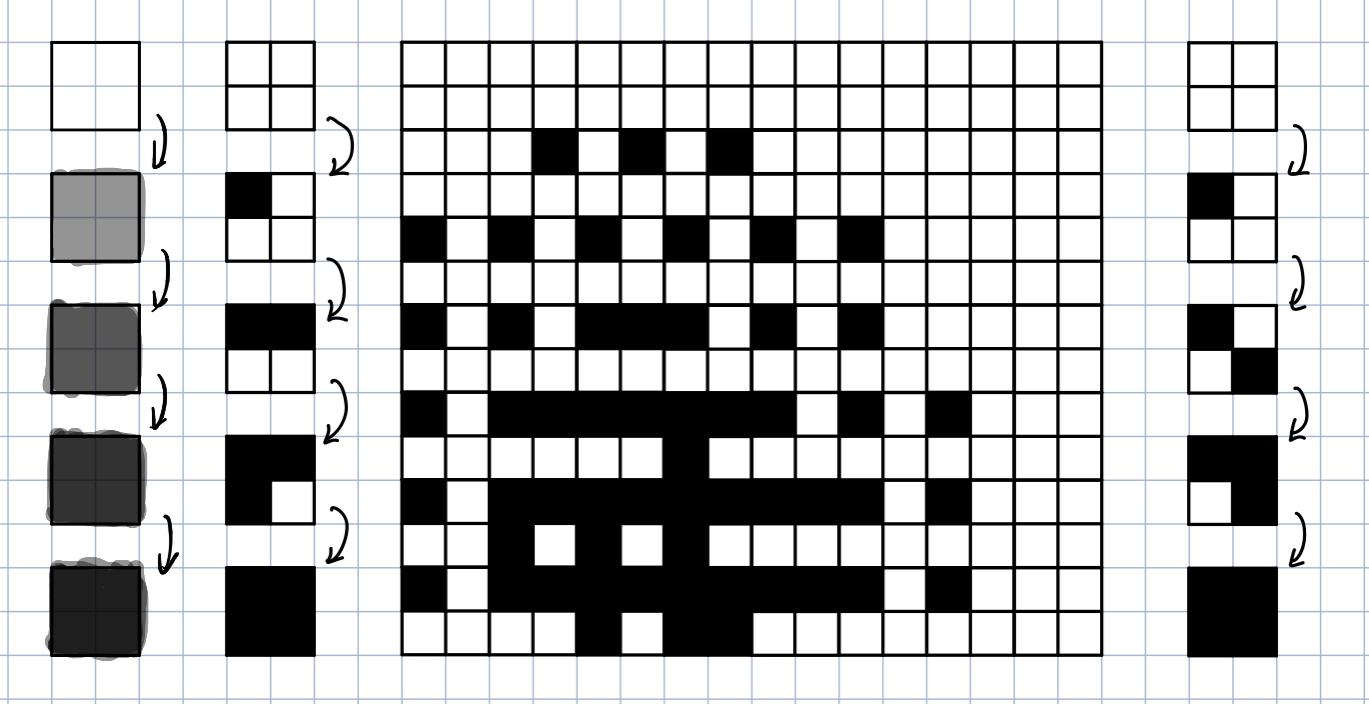
这一过程的本质是用空间换取色彩深度，利用人眼的的空间低通滤波效果来模仿灰度，提升显示效果，这一原理颇有电学中“脉宽调制”的意味。

在这样的规则抖动算法中，仿色矩阵中色块的排布方式对最终效果有着重要影响，显而易见，矩阵中的色块应尽量分布均匀，而不是集中在一起（联想：脉宽调制、改进脉宽调制及Sigma-Delta调制）。一种简单巧妙的分散方法如上图右侧一列所示：对于2×22{\times}2仿色矩阵，灰度由低到高，先填充对角块，再填充剩下的块，使用矩阵描述即是：

M1=[0231]M_1= \begin{bmatrix} 0 & 2 \\ 3 & 1 \\ \end{bmatrix}

可见2×22{\times}2即2阶仿色矩阵，可模仿5级灰度，那么，要是想模拟跟多级灰度，仿色矩阵该如何得到呢？还是按照对角线先行的思路，递推可得：

M2=[0821012414631119157135]M_2= \begin{bmatrix} 0 & 8 & 2 & 10 \\ 12 & 4 & 14 & 6 \\ 3 & 11 & 1 & 9 \\ 15 & 7 & 13 & 5 \\ \end{bmatrix}

可以得出递推公式：

Mn+1=[4Mn4Mn+2Un4Mn+3Un4Mn+Un]M_{n+1}= \begin{bmatrix} 4M_n & 4M_n + 2U_n \\ 4M_n + 3U_n & 4M_n + U_n \\ \end{bmatrix}

其中，M3M_3即8阶仿色矩阵实用较多，被称为Bayer矩阵，Bayer抖动算法由此而来。

下图是一组M2M_2规则抖动的效果[6]，可以看出像素分布变化具有明显的规律，若原图像存在大片灰度相同或相近的区域，仿色图案也会在此重复排布，形成明显的线条感，对观感有很大的影响，这也是规则抖动的缺陷。

3-3

可见，人眼也对周期重复的图案十分敏感，和耳朵一样具有“傅里叶变换”的特性呢。

3-4

不过，得益于规则抖动较为简单的算法（以比较运算为主），且可针对单一像素使用，其运行速度很快。下面是在一块128*64像素的OLED显示屏上，使用Bayer抖动算法显示热成像传感器输出的8*8像素（灰度）热力图的效果：

3-5

全系统由一片48MHz的Cortex-M0微控制器实现，热力图流帧数可达20以上，显示效果很好。

3-6

3.2.Floyd–Steinberg抖动

Floyd–Steinberg抖动算法是一种误差扩散算法：先将处理的第一个像素点与阈值比较，得到量化后的像素值，将原像素值与量化像素值相减，得到量化误差，将这个误差按照一定比例加到周围的像素点上，再进行下一个像素点的比较、量化，重复执行。Floyd–Steinberg抖动算法使用的误差扩散权重如下：

[∗716......316516116...]\begin{bmatrix} & & * & \frac{7}{16} & ... \\ ... & \frac{3}{16} & \frac{5}{16} & \frac{1}{16} & ... \\ \end{bmatrix}

如同滴入清水中的墨汁的扩散，每个像素点的量化误差实际会扩散至其后的所有像素，最终，体现出一种较为自然的平滑效果。算法的实现使用Matlab语言可以较为简洁，如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
for y = 1 : Y_SIZE - 1
    for x = 1 + 1 : X_SIZE - 1
        oldRGB = double(ditherImg(y, x, :));
        newRGB = round(oldRGB .* (scale / 255)) .* (255 / scale);
        ditherImg(y, x, :) = newRGB; 
        errRGB = double(oldRGB - newRGB);
        ditherImg(y + 0, x + 1, :) = double(ditherImg(y + 0, x + 1, :)) + errRGB .* (7/16.0);
        ditherImg(y + 1, x - 1, :) = double(ditherImg(y + 1, x - 1, :)) + errRGB .* (3/16.0);
        ditherImg(y + 1, x + 0, :) = double(ditherImg(y + 1, x + 0, :)) + errRGB .* (5/16.0);
        ditherImg(y + 1, x + 1, :) = double(ditherImg(y + 1, x + 1, :)) + errRGB .* (1/16.0);
    end
end

使用灰度模式，2bit量化：

3-7

使用彩色模式，2bit量化：

3-8

使用彩色度模式，4bit量化，在PC98时期，很多游戏都采用了16级色彩，即4bit，左图直接量化的效果可以说是稍有“PC98风了”，若如右图应用Floyd–Steinberg抖动，画面效果的提升还是明显的。

3-9

Floyd–Steinberg抖动不会产生连续规则的条纹，不需要牺牲像素点数，平滑效果良好，可以说是十分出色的抖动算法。不过，误差扩散原理也意味着，一个像素点的改变会带来其他大量像素点的重新计算，在处理视频时代价巨大，且算法中包含大量乘加。因此，Floyd–Steinberg抖动并没像规则抖动那样应用广泛。

同时可以注意到，Floyd–Steinberg抖动会带来许多离散的点，即使在原图的大片空白处也会出现，且呈现出规律排布，这也是误差扩散带来的特性，在图像分辨率较低时，可能对观感有较大的影响：

3-10

但它仍不失为一个巧妙而成功的算法。此后，又有许多学者基于Floyd–Steinberg算法作出了改进，在显示效果及运行效率上进行优化[5]：

3-11

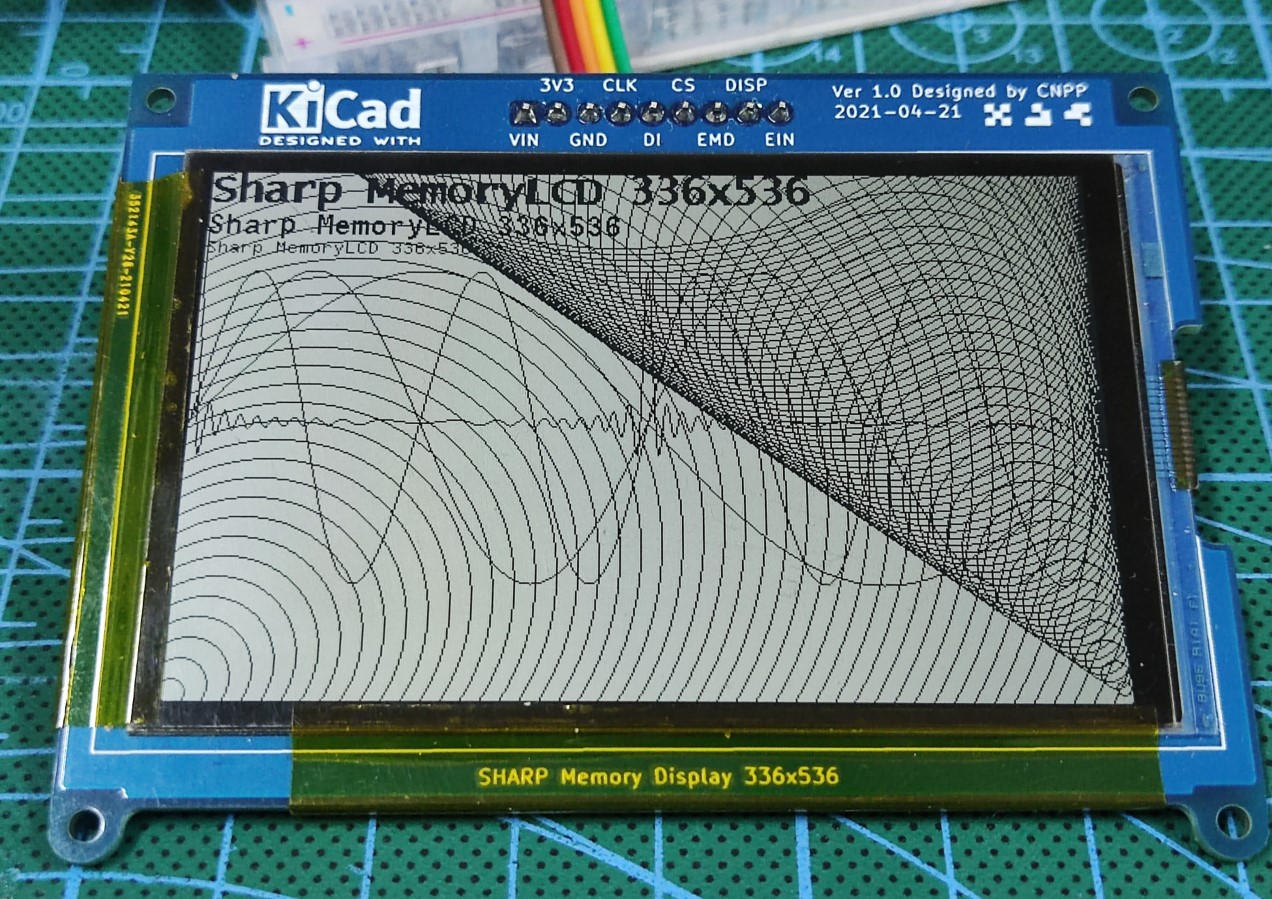
最后是在MemoryLCD上使用Floyd–Steinberg抖动实现的频谱显示效果：

3-12

以及利用误差扩散思想，仅在一维作扩散，得到的效果，使用此方法实现瀑布图显示预期会得到更好的效果：

3-13

4.总结

如今，随着软硬件技术的发展，屏幕、存储越来越难以阻止数字图像的绚烂，抖动技术也渐渐淡出了主流显示领域。但是在低功耗、便携设备的领域，它依然以各种方式，在有限的硬件机能下为我们提升观感。

此外，抖动算法依然活跃于以像素风格为主题的美术、游戏作品之中，为复古的艺术带来和谐的视觉提升。

拍一幅GameBoy风格的照片：

4-1

像素风格极短RPG解谜作品《噬人白昼》[7]：

4-2

5.参考

[1] Ken C. Pohlmann (2005). Principles of Digital Audio. McGraw-Hill Professional. ISBN 978-0-07-144156-8.
[2] Deutsch, Diana (1999). The psychology of music. Gulf Professional Publishing. p. 153. ISBN 978-0-12-213565-1. Retrieved 24 May 2011.
[3] Hauser, Marc D. (1998). The evolution of communication. MIT Press. p. 190. ISBN 978-0-262-58155-4. Retrieved 24 May 2011.
[4] Montgomery, Christopher (Monty) (2012–2013). “Digital Show and Tell”. Xiph.Org / Red Hat, Inc. Retrieved 27 February 2013. “Dither is specially-constructed noise that substitutes for the noise produced by simple quantization. Dither doesn’t drown out or mask quantization noise, it replaces it with noise characteristics of our choosing that aren’t influenced by the input.”
[5] Wikipedia. Dither. https://en.wikipedia.org/wiki/Dither#cite_note-Deutsch1999-9
[6] Wikipedia. Ordered dithering. https://en.wikipedia.org/wiki/Ordered_dithering
[7] 《噬人白昼》. congwsbn. https://rpg.blue/?317370

1

$$ $$

欢迎关注我的其它发布渠道